Question

Suppose that the functions u and w are defined as follows.u(x) = x +7w(x) = x+8

Answer 1

`\begin{gathered} u(x)=x^2+7 \\ w(x)=\sqrt[]{x+8} \end{gathered}`

To find the value of the composed function (u ∘ w) evaluated in 1, we need to compose the functions.

`(u\circ w)=u(w(x))`

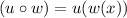
This means wherever we have x in the function u, we need to replace it with the expression for w(x) as follows:

`\begin{gathered} (u\circ w)=u(w(x))=w(x)^2+7 \\ \\ (u\circ w)=(\sqrt[]{x+8})^2+7 \end{gathered}`

Solving the squared expression:

`\begin{gathered} (u\circ w)=x+8+7 \\ \\ (u\circ w)=x+15 \end{gathered}`

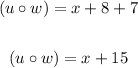
Now we know the composed function. We just need to evaluate it in x = 1, that is, replace 1 wherever the function has an x:

`\begin{gathered} (u\circ w)(1)=1+15 \\ \\ (u\circ w)(1)=16 \end{gathered}`

Now we have the first answer: (u ∘ w)(1) = 16.

To find the value of (w ∘ u)(1) we follow the same logic:

`(w\circ u)=w(u(x))`

In the function w, wherever we have an x, we replace it by the expression for u(x):

`\begin{gathered} (w\circ u)=w(u(x))=\sqrt[]{u(x)+8} \\ \\ (w\circ u)=\sqrt[]{(x^2+7)+8}=\sqrt[]{x^2+7+8} \\ \\ (w\circ u)=\sqrt[]{x^2+15} \end{gathered}`

Now we know the composed function (w ∘ u). We just need to evaluate it in x = 1, that is, replace 1 wherever the function has an x:

`\begin{gathered} (w\circ u)(1)=\sqrt[]{1^2+15}=\sqrt[]{1^{}+15} \\ \\ (w\circ u)(1)=\sqrt[]{16} \\ \\ (w\circ u)(1)=4 \end{gathered}`

Now we have the second answer: (w ∘ u)(1) = 4.