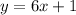Given the equation of the line in slope-intercept form:

where 'm' defines the slope of the line, we can find the perpendicular slope using the following expression:
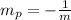
In this case, we have the following equation of the line:
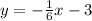
notice that the slope is m = -1/6. Then, using the expression for the perpendicular slope, we have:
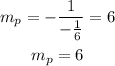
therefore, the equation of the line that is perpendicular to y = -1/6x - 3 is: