We are given the following equation
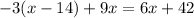
Let us solve the equation for x.
Step 1:
Multiply the term -3 with the terms in the parenthesis.
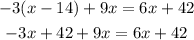
Step 2:
Simplify the terms on the left-hand side of the equation
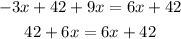
Step 3:
Combine the like terms together.
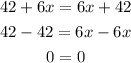
This means that this equation has an infinite number of possible solutions.
If you notice the left and right side of the equation are exactly the same.
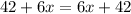
This means that whatever value of x you put into this equation, the equation will always be satisfied.
Try substituting some values for x.
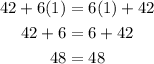
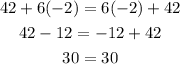
Hence, the given equation has an infinite number of possible solutions.