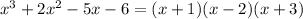Question

Find the Real Zeros of F and use the real zeros to factor f.

Answer 1

Solving a third-degree equation implies testing some possible solutions until we find them all.

The equation to solve is:

`x^3+2x^2-5x-6=0`

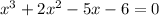
Dividing the factors of the independent coefficient by the factors of the leading coefficient will give us some candidates solutions:

+/- 6, +/-3, +/- 2, +/- 1

Testing x = -1

`\begin{gathered} (-1)^3+2(-1)^2-5(-1)-6=0 \\ \\ -1+2+5-6=0 \\ \\ 0=0 \end{gathered}`

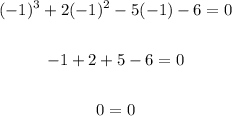
The equation is verified, so x = -1 is a solution.

Testing x = 1

`\begin{gathered} (1)^3+2(1)^2-5(1)-6=0 \\ \\ 1+2-5-6=0 \\ \\ -8=0 \end{gathered}`

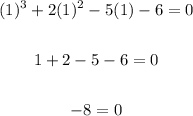
The equation does not verify, so x = 1 is not a solution.

Testing x = 2

`\begin{gathered} (2)^3+2(2)^2-5(2)-6=0 \\ \\ 8+8-10-6=0 \\ \\ 0=0 \end{gathered}`

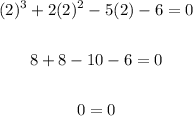
x = 2 is a solution.

Finally, testing x = -3

`\begin{gathered} (-3)^3+2(-3)^2-5(-3)-6=0 \\ \\ -27+18+15-6=0 \\ \\ 0=0 \end{gathered}`

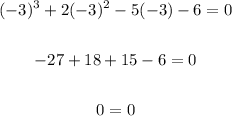
The real zeros are x = -1, x = 2, x = -3.

Factoring:

`x^3+2x^2-5x-6=(x+1)(x-2)(x+3)`