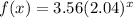From the given table, let's find an exponential function to model the data.
To write the exponential function, apply the formula:
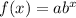
Where:
b is the rate of change.
We have:
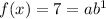
Now substitute (7, 522) for the values of x and f(x):
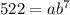
Divide both equations to find b:
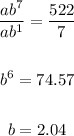
The value of b is 2.04.
To find the value of a, we have:
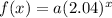
Substituet (7, 522) for values of x and f(x):
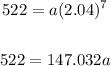
Divide both sides by 147.032a:
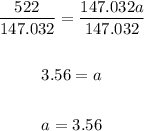
Therefore, the exponential function to model the data is:
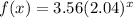
ANSWER: