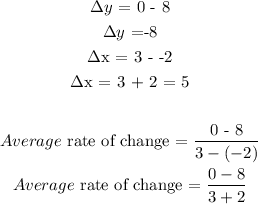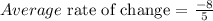Question

The function y=f(x) is graphed below. Plot a line segment connecting the points on ff where x=-2 and x=3. Use the line segment to determine the average rate of change of the function f(x) on the interval −2≤x≤3

Answer 1

Answer:

Δy = -8

Δx = 5

Average rate of change = -8/5

Step-by-step explanation:

Given:

The graph of y = f(x)

To find:

The average rate of change oer the interval− 2≤x≤3

`\begin{gathered} Average\text{ rate of change is given as: }\frac{f(b\text{ - a\rparen}}{b\text{ - a}} \\ where\text{ a\le x\le b is the interval} \\ −2≤x≤3:\text{ a =-2, b = 2} \\ \\ Based\text{ on the formula we are given in the question:} \\ Average\text{ rate of change = }(\Delta y)/(\Delta x) \end{gathered}`

When x = -2

f(x) = 8

when x = 3

f(x) = 0

We will connect the vlus of both f(x)with a line

`\begin{gathered} \Delta y\text{ = 0 - 8} \\ \Delta y\text{ =-8} \\ \Delta\text{x = 3 - \lparen-2\rparen} \\ \Delta\text{x = 3 + 2 = 5} \\ \\ Average\text{ rate of change = }\frac{0\text{ - 8}}{3-(-2)} \\ Average\text{ rate of change = }(0-8)/(3+2) \end{gathered}`
`Average\text{ rate of change = }(-8)/(5)`