Question

Find: when is the acceleration positive, and when is it negative?Given:

Answer 1

They ask for the sign of the acceleration of a moving object, and its position function is:

`s(t)=t^{(5)/(2)}(7-t)`

0<= t <=20

Remember that we can know both, the velocity and the acceleration function from the before equation. Because the velocity is the derivate of the position, and the acceleration is the derivate of the velocity, then we have:

`v(t)=(5)/(2)t^{(3)/(2)}-(7)/(2)t^{(5)/(2)};\text{ }0\leq t\leq20`

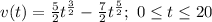
And the acceleration:

`a(t)=(15)/(4)t^{(1)/(2)}-(35)/(4)t^{(3)/(2)};\text{ }0\leq t\leq20`

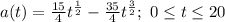
Now we need to solve the inequality:

`(15)/(4)t^{(1)/(2)}-(35)/(4)t^{(3)/(2)}<0`
`(5)/(4)t^{(1)/(2)}(3-7t)<0`
`t>(3)/(7)`

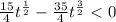
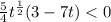
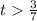
And as 0<=3/7<=20, we can say that the acceleration will be negative in the interval:

`((3)/(7),20]`

Now we can directly infer when the acceleration will be positive, but let´s still check mathematically:

`(5)/(4)t^{(1)/(2)}(3-7t)>0`
`3-7t>0`
`t<(3)/(7)`

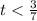
And as 0<=3/7<=20, we can say that the acceleration will be positive in the interval:

`{}{}{}{}\lbrack0,(3)/(7))`

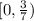
So, we can conclude that the summary of answers is:

Acceleration positive:

`{}{}{}{}\lbrack0,(3)/(7))`

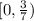
Acceleration negative:

`((3)/(7),20]`