VARIABILITY
Variability (also called spread or dispersion) refers to how spread out a set of data is. Variability gives you a way to describe how much data sets vary and allows you to use statistics to compare your data to other sets of data.
The variability can be analyzed using the range. The range is the amount between your smallest and largest item in the set. You can find the range by subtracting the smallest number from the largest.
Range of Quiz 1
Highest score: 91
Lowest score: 70
Therefore, the range is:

Range of Quiz 2
Highest score: 96
Lowest score: 75
Therefore, the range is:
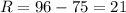
Therefore, the variability of both quizzes is the same.
MEAN
The mean is a measure of central tendency of a probability distribution along median and mode. It is also referred to as an expected value.
It can be calculated as the total sum of all values in a collection of numbers divided by the number of numbers in a collection. Therefore, the formula is:
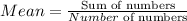
Mean of Quiz 1
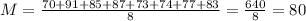
Mean of Quiz 2
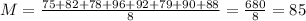
Therefore, the mean of Quiz 2 is greater than that for Quiz 1.
ANSWER
The correct option is OPTION C: The mean of Quiz 2 scores is greater than the mean of Quiz 1 scores, but the variability is the same.