Question

Enumerate all the numbers in the power of 3 which are in the ones digit, and then find the next seven terms in the sequence without getting the power of 3.

Answer 1

hello

to find the powers of 3 which are 1 single digit, let's check them out

`\begin{gathered} 3^1=3 \\ 3^2=9 \\ 3^3=27 \end{gathered}`

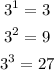
from the calculation above the numbers which are one single digit are only 3 and 9 and their powers are 1 and 2 respectively

question 2

the next seven terms witout getting the power of 3

we'll start first by identifying what type of sequence is this and proceed accordingly to solve

first term = 3

second term = 9

this is a geometric sequence

to find the 3rd, 4th, 5th....7th term, let's use the formula for gp

`T_n=ar^(n-1)`

for 3rd term

a = first term

r = common ratio = 9/3 = 3

`\begin{gathered} T_3=ar^(3-1) \\ T_3=3*3^2 \\ T_3=27 \end{gathered}`
`\begin{gathered} T_4=ar^3 \\ T_4=3*3^3 \\ T_4=81 \end{gathered}`
`\begin{gathered} T_5=ar^4 \\ T_5=3*3^4 \\ T_5=243 \end{gathered}`
`\begin{gathered} T_6=ar^5 \\ T_6=3*3^5 \\ T_6=729 \end{gathered}`
`\begin{gathered} T_7=ar^6 \\ T_7=3*3^6 \\ T_7=2187 \end{gathered}`
`\begin{gathered} T_8=ar^7 \\ T_8=3*3^7 \\ T_8=6561 \end{gathered}`
`\begin{gathered} T_9=ar^8 \\ T_9=3*3^8 \\ T_9=19683 \end{gathered}`

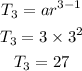
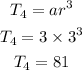
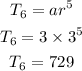
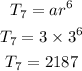
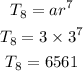
from the calculation, the next seve terms are 81, 243, 729, 2187, 6561 and 19683