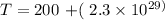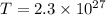Question

If you deposit $200 into an account that pays 9% annual interest compounded weekly, how much money willyou have after 8 years?

Answer 1

To calculate the compound interest is;

`A=P\lbrack1+(r)/(n)\rbrack^(nt)`

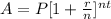
A is the ending amount

P is the principal

r is the interest rate

n is the number of compoundings a year

T is the time frame

From the question;

P= $200

R=9

Since it is compounded weekly, then n is 52

T=8

substituting into the formula;

`A=200\lbrack1+(9)/(52)\rbrack^(52*8)`

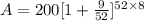
Evaluating;

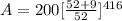
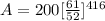
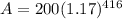
`A=200\lbrack(52+9)/(52)\rbrack^(416)`

`A=200\lbrack(61)/(52)\rbrack^(416)`
`A=200(1.17)^(416)`

A=

`A=2.3*10^(29)`

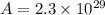
T= P+A

`T=200\text{ +( 2.3}*10^(29))`
`T=2.3*10^(27)`