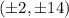Question

Hi please can I get help finding the P coordinates as I’m stuck with the second half of the question

Answer 1

First there's some correction in your solution

`(dy)/(dx)=3x^2-11`

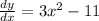
and you have put value x=3 in

`\begin{gathered} (dy)/(dx)=3x^2 \\ (dy)/(dx)=3*3^2 \\ (dy)/(dx)=27 \end{gathered}`

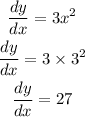
the correct calculation will be,

`\begin{gathered} (dy)/(dx)=3x^2-11 \\ (dy)/(dx)=3*3^2-11 \\ (dy)/(dx)=27-11 \\ (dy)/(dx)=16 \end{gathered}`

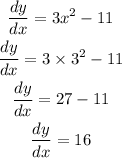
Now, answer of the (b) part is,

Given curve is,

`y=x^3-11x+1`

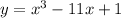
and point P lies on C and the gradient at that point is 1.

We will take point P on curve C as

`(x_(1,)y_1)`

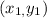
Put point P in curve C, we will get,

`y_1=x_1^3-11x_1+1`

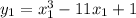
Now, we will differentiate

`y_1`

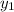
we will get,

`(dy)/(dx)=3x^2_1-11_{^{^{}}}`

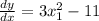
Now, we have given that gradient at point P is 1,

`\begin{gathered} 1=3x^2_1-11 \\ 3x^2_1=12 \\ x^2_1=4 \\ x_1=\pm2 \end{gathered}`

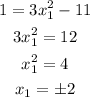
corresponding these points we will get y=

`\pm14`

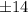
So, possible co-ordinate of P is

`(\pm2,\pm14)`