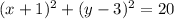Question

The point (1,4) and(-3,2) are the endpoints of a diameter of a circule.What IS the equation of the circle?

Answer 1

The endpoints of a diameter of a circle are

`(1,4)\: and\: (-3,2)`

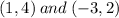
Recall that the equation of a circle is given by

`(x-h)^2+(y-k)^2=r^2`

Where (h, k) are the coordinates of the center of the circle and r is the radius of the circle.

The coordinates of the center of the circle (h, k) can be found using the midpoint formula.

`\begin{gathered} (h,k)=((x_1+x_2)/(2),(y_1+y_2)/(2)) \\ (h,k)=(\frac{1_{}+(-3)_{}}{2},\frac{4_{}+2}{2}) \\ (h,k)=(\frac{1_{}-3_{}}{2},\frac{4_{}+2}{2}) \\ (h,k)=(\frac{-2_{}}{2},(6)/(2)) \\ (h,k)=(-1,3) \end{gathered}`

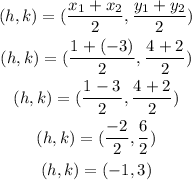
So, the center of the circle is at (-1, 3)

The radius of the circle can be found using the distance formula

`\begin{gathered} r=\sqrt{\left( {x_2 - x_1 } \right)^2 + \left( {y_2 - y_1 } \right)^2 } \\ r=\sqrt[]{({-3-1_{}})^2+({2_{}-4})^2} \\ r=\sqrt[]{({-4_{}})^2+({-2})^2} \\ r=\sqrt[]{16^{}+4^{}} \\ r=\sqrt[]{20} \end{gathered}`

So, the radius of the circle is √20

Finally, let us write the equation of the circle

`\begin{gathered} (x-h)^2+(y-k)^2=r^2 \\ (x-(-1))^2+(y-3)^2=(\sqrt[]{20}^{})^2 \\ (x+1)^2+(y-3)^2=20^{} \end{gathered}`

Therefore, the equation of the circle is

`(x+1)^2+(y-3)^2=20^{}`