Question

a merry go round has a radius of 18 ft if a passenger gets on a horse located at the edge of thevwheel and travels 38 ft find the angle of rotation to the nearest degree

Answer 1

Angle of rotation for the merry go round = 121°

Step-by-step explanation

The distance travelled by the wheel by moving/rotating through an angle is the length of the arc that would subtend the angle moved through at the center of the circle.

`\text{Length of an arc = }(\theta)/(360\degree)*2\pi r`

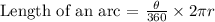
where

Length of the arc = 38 ft.

θ = Angle that the circular figure moves through = ?

π = pi = 3.14

r = radius of the circle involved in the motion = 18 ft.

`\begin{gathered} \text{Length of an arc = }(\theta)/(360\degree)*2\pi r \\ \text{38 = }(\theta)/(360\degree)*2\pi*(18) \\ 38=0.3143\theta \end{gathered}`

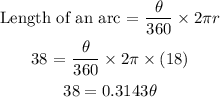
We can rewrite this as

0.3143θ = 38

Divide both sides by 0.3143

(0.3143θ/0.3143) = (38/0.3143)

θ = 120.9° = 121° to the nearest degree.

Hope this Helps!!!