Question

In ADEF, DF = 16 and m

Answer 1

Let's put more details in the given figure to better understand the problem:

It appears that the triangle is an Isosceles Triangle. Because of this, the legs of the triangle should be congruent.

Let's determine the length of its leg using the Sine Function: Let, x = the length of the leg.

`\text{ Sine }\Theta\text{ = }\frac{\text{ Opposite}}{\text{ Hypotenuse}}`
`\text{ Sine }45^(\circ)\text{ = }\frac{\text{ x}}{\text{ 1}6}`
`\text{ (16)Sine }45^(\circ)\text{ = x}`
`\text{ x = (16)Sine }45^(\circ)`
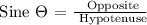
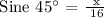
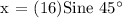
`\text{ x = (16)(}\frac{1}{\sqrt[]{2}})\text{ = }\frac{16}{\sqrt[]{2}}\text{ = }\frac{\text{ 16 }\cdot\text{ }\sqrt[]{2}}{\sqrt[]{2}\text{ }\cdot\text{ }\sqrt[]{2}}\text{ = }\frac{16\sqrt[]{2}}{2}`
`\text{ x = 8}\sqrt[]{2}`

Therefore, the length of its leg is 8√2