Question

3 6x-27-62 3x-29-4z=8 3x-224-26e) -axt62=-16lds 21-22=-2620 or-st3t=-9 5r + 5s - 5t = 20 3r-s+4+=-5

Answer 1

In this question we will solve the following system of equations by elimination:

`\begin{cases}6r-s+3t=-9 \\ 5r+5s-5t=20 \\ 3r-s+4t=-5 \\ \end{cases}`

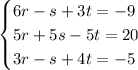
In order to solve this system by elimination, let's divide the second equation by 5 and then add it to the first and third equations:

`\begin{gathered} 5r+5s-5t=20 \\ r+s-t=4 \\ \\ 6r-s+3t+(r+s-t)=-9+4 \\ 7r+2t=-5 \\ \\ 3r-s+4t+(r+s-t)=-5+4 \\ 4r+3t=-1 \end{gathered}`

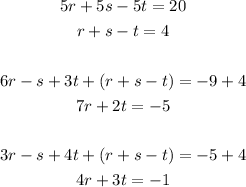
Now, let's multiply the equation (7r + 2t = -5) by 3 and the equation (4r + 3t = -1) by -2, and then add them:

`\begin{gathered} 21r+6t=-15 \\ -8r-6t=2 \\ \\ 21r+6t+(-8r-6t)=-15+2 \\ 13r=-13 \\ r=-1 \end{gathered}`

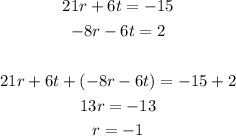
From the equation 4r + 3t = -1, we have:

`\begin{gathered} -4+3t=-1 \\ 3t=3 \\ t=1 \end{gathered}`

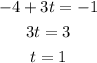
From the equation r + s - t = 4, we have:

`\begin{gathered} -1+s-1=4 \\ s=4+1+1 \\ s=6 \end{gathered}`

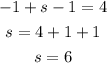
So the solution is r = -1, s = 6 and t = 1.