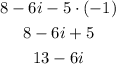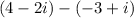
When we are working with imaginary numbers, it is like working with an algebraic expression in which i will be the variable and can only added or substracted with expressions with the same variable i.
To solve this problem add all number without the i and also add all numbers with the imaginary portion.
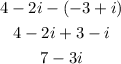
When we talk about the product between imaginary numbers, we apply the same principal for algebraic however we mus remember the power derived from the i, here are some examples.
![\begin{gathered} i=\sqrt[]{-1} \\ i^2=(\sqrt[]{-1})^2=-1 \\ i^3=(\sqrt[]{-1})^3=-\sqrt[]{-1}=-i \\ i^4=(\sqrt[]{-1})^4=1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/5zxxfikni0fjjgt354wao7wkvzn7d79ze8.png)
remembering this, start by solving the product
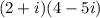
distribute the factors
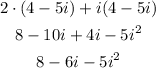
apply the powers for i