Solution:
Given:
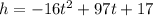
when the height is 71ft,
h = 71
Hence,
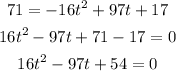
Using the quadratic formula;
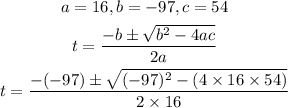
Hence,
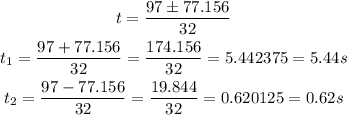
Therefore, the height will be 71 feet at 5.44 seconds or 0.62 seconds.
The object will reach the ground at;
The object will reach the height of 17ft at;
h = 17
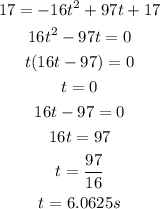
Hence, the time it will take to reach the ground will be the time it takes to go up and return back to the ground;
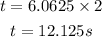
It will take 12.125 seconds for the object to reach the ground.