We need to find the average velocity at each time interval.
The average velocity ΔV is the change in position at two moments divided by the change of time:
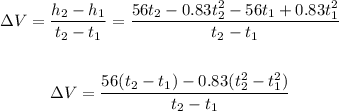
Using the above formula for each interval, we find:
• [7,8]:
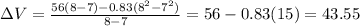
• [7,7.5]:

• [7,7.1]:
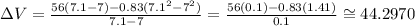
• [7,7.01]:
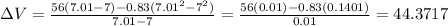
• [7,7.001]:
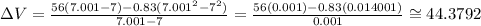
Therefore, the average velocities are:
[7,8]: 43.55 m/s
[7,7.5]: 43.965 m/s
[7,7.1]: 44.2970 m/s
[7,7.01]: 44.3717 m/s
[7,7.001]: 44.3792 m/s