Question

Two similar pyramids have slant height of 4 and 6. 1. Find the scale factor. 2. If the volume of the smaller pyramid is 48m cubed, what is the volume of the larger pyramid?

Answer 1

We are given two similar pyramids and told they have slant height of 4 and 6

Let's focus on the face of the pyramid formed by 2 slant heights and a side of the base.

Since the pyramids are similar, these triangles will also be similar.

From here, we divide the lenght of the side of the larger triangle by the lenght of the side of the smaller triangle to see how much bigger the sides are in comparisson.

So

`(6)/(4)=(3)/(2)=1.5`

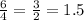
So the sides of the larger triangle are 1.5 times bigger than the sides of the smaller triangle.

Now, the formula to get the volume of a pyramid is

`V=(1)/(3)\cdot A_{}\cdot h`

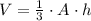
Where A is the area of the base and h is it's heigh. Note that this height is different from the slant height.

However, since the pyramids are similar, their height will also be proportional by a factor of 1.5.

The volume of the smaller pyramid will be

`V_1=(1)/(3)\cdot l\cdot l\cdot h`

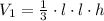
Where l is the lenght of the side of the base.

Now, the volume of the larger pyramid, taking into account the 1.5 scale factor of its sides will be

`V_2=(1)/(3)\cdot(l\cdot1.5)\cdot(l\cdot1.5)\cdot(h\cdot1.5)`

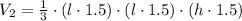
Let's compare volumes 1 and 2 as follows:

`(V_2)/(V_1)=((1)/(3)l^2\cdot(1.5)^3\cdot h)/((1)/(3)l^2\cdot h)=(1.5)^3=3.375`

So, the volume of the larger pyramid will be 3.375 times larger than the volume of the smaller pyramid.

Furthermore, we are told the volume of the smaller pyramid is 48, so we can replace this vale on the above equation to find the volume of the larger pyramid:

`(V_2)/(48)=3.375`
`V_2=48\cdot3.375=162`

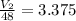
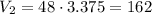
And so, the volume of the larger pyramid is 162.