Answer:
The dimensions of the box so that total costs are minimum are a side length of 2 feet and a height of 5 feet.
Explanation:
Geometrically speaking, the volume of the rectangular box (
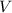 ), in cubic feet, is represented by this formula:
), in cubic feet, is represented by this formula:
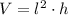 (1)
(1)
Where:
 - Side length of the box, in feet.
- Side length of the box, in feet.
 - Height of the box, in feet.
- Height of the box, in feet.
In addition, the total cost of the box (
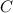 ), in monetary units, is defined by this formula:
), in monetary units, is defined by this formula:
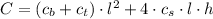 (2)
(2)
Where:
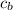 - Unit cost of the base of the box, in monetary units per square foot.
- Unit cost of the base of the box, in monetary units per square foot.
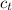 - Unit cost of the top of the box, in monetary units per square foot.
- Unit cost of the top of the box, in monetary units per square foot.
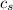 - Unit cost of the side of the box, in monetary units per square foot.
- Unit cost of the side of the box, in monetary units per square foot.
By (1), we clear
 into the expression:
into the expression:
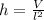
And we expand (2) and simplify the resulting expression:
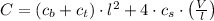 (3)
(3)
If we know that
 ,
,
 ,
,
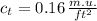 and
and
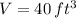 , then we have the resulting expression and find the critical values associated with the side length of the base:
, then we have the resulting expression and find the critical values associated with the side length of the base:
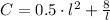
The first and second derivatives of this expression are, respectively:
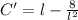 (4)
(4)
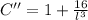 (5)
(5)
After equalizing (4) to zero, we solve for
 : (First Derivative Test)
: (First Derivative Test)
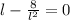
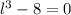
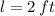
Then, we evaluate (5) at the value calculated above: (Second Derivative Test)
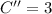
Which means that critical value is associated with minimum possible total costs. By (1) we have the height of the box:
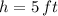
The dimensions of the box so that total costs are minimum are a side length of 2 feet and a height of 5 feet.