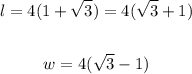We have the following situation:
• The diagonal of a rectangle is equal to 8√2 inches.
,
• The width is 8 inches less than the length
And we need to find the dimensions of the rectangle.
Then we can proceed as follows:
1. We know that all the internal angles of a rectangle are right angles, and the diagonals are congruent. We also know that the width of this rectangle is 8 inches less than the length:
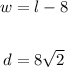
2. Then we can draw the situation as follows:
3. Now, we can apply the Pythagorean Theorem as follows:
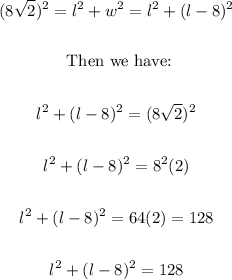
4. We have to expand the binomial expression on the left side of the equation:
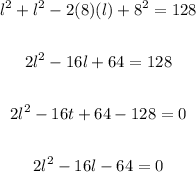
5. Now, we need to apply the quadratic formula to find the value of l as follows:
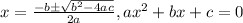
6. Then we have that:
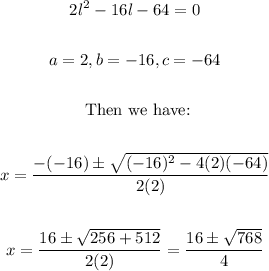
7. Now, to simplify the radicand, we need to find the factors of 768:
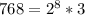
Now, we have:

8. Then the values for l are two possible ones:
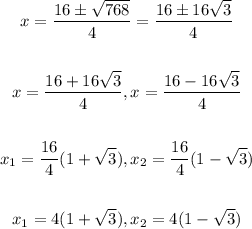
We can see that x2 gives us a negative value, and since we are finding a length, which is a positive value, then the value for l is:

9. Now, we have that:
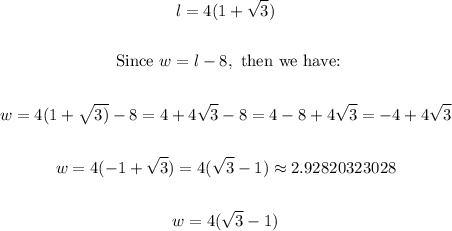
10. Now, we can check both values as follows:
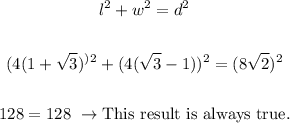
Therefore, in summary, the dimensions of the rectangle are: