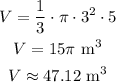Question

For the accompanying right circular cone, h = 5 m and r = 3 m. Find the exact and approximate measures (rounded to two decimal places, using your calculator value of ) for each of the following.A circular cone has a right angle between an altitude labeled h and a radius labeled r.(a)lateral area (in square meters)exactm2approximatem2(b)total area (in square meters)exactm2approximatem2(c)volume (in cubic meters)exactm3approximatem3

Answer 1

(a) Exact lateral area:

`3√(34)\pi\text{ m}^2`

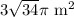
Approximate lateral area:

`54.96\text{ m}^2`

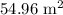
(b) Exact total area:

`\begin{equation*} 9\pi+3√(34)\pi\text{ m}^2{} \end{equation*}`

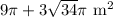
Approximate total area:

`\begin{equation*} 83.23\text{ m}^2 \end{equation*}`

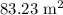
(c) Exact volume:

`\begin{equation*} 15\pi\text{ m}^3 \end{equation*}`

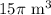
Approximate volume:

`\begin{equation*} 47.12\text{ m}^3 \end{equation*}`

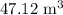
Explanation

Lateral area of a cone formula

`LA=\pi r{√(h^2+r^2)}`

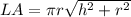
where r is the radius and h is the height of the cone.

Substituting h = 5 m, and r = 3 m, we get:

`\begin{gathered} LA=\pi\cdot3\cdot√(5^2+3^2) \\ LA=3√(34)\pi\text{ m}^2 \\ LA\approx54.96\text{ m}^2 \end{gathered}`

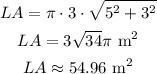
Total area of a cone formula

`TA=\pi r^2+LA`

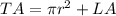
Substituting with the previous result and r = 3 m, we get:

`\begin{gathered} TA=\pi\cdot3^2+3√(34)\pi \\ TA=9\pi+3√(34)\pi\text{ m}^2{} \\ TA\approx83.23\text{ m}^2 \end{gathered}`

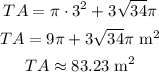
Volume of a cone formula

`V=(1)/(3)\pi r^2h`

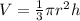
Substituting h = 5 m, and r = 3 m, we get:

`\begin{gathered} V=(1)/(3)\cdot\pi\cdot3^2\cdot5 \\ V=15\pi\text{ m}^3 \\ V\approx47.12\text{ m}^3 \end{gathered}`