There is a total of n! ways of arranging n elements on a list. In this case, the word "GATHERINGS" has 10 letters. Nevertheless, two of them are the same letter (there are two "G"s), then, half of those combinations are repeated.
Then, there is a total of 10!/2 ways to arrange those letters. Use a calculator to find the value of 10!/2:
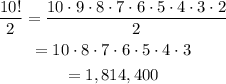
Therefore, the total amount of ways in which the letters on the word "GATHERINGS" can be arranged, is:
