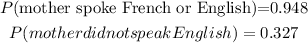From the given values, the probability that a mother speak French or English is given by
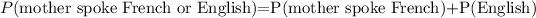
because the event "speak French" is independent of the event "speak English". By substituting the given values, we get
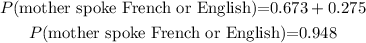
On the other hand,
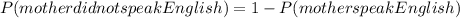
which igives
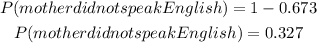
Therefore, the answer are