Question

The floor of a one-story building is 14 feet longer than it is wide(w). The building has1632 square feet of floor space.(a) Write a Quadratic Equation for the area of the floor in terms of w.(b) Find the length and width of the floor.

Answer 1

a) w^2+14w-1632 = 0

b) Length = 48 feet

Width = 34 feet

Explanations:

a) Let the floor of the one-story building be a rectangle. The formula to calculate the area of the floor is expressed as;

`A=lw`

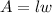
where;

l is the length of the storey building

w is the width of the one-storey building

If the floor of a one-story building is 14 feet longer than it is wide(w), hence;

`l=w+14`

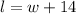
Substitute the length function into the area of the floor to have;

`\begin{gathered} A=(w+14)w \\ A=w^2+14w \\ \end{gathered}`

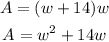
If the building has 1632 square feet of floor space, hence the area of the floor will be expressed as;

`\begin{gathered} 1632=w^2+14w \\ \text{Swap} \\ w^2+14w=1632 \\ w^2+14w-1632=0 \end{gathered}`

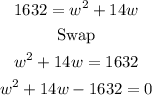
b) To get the length and width of the floor, we will factorize the quadratic expression to have;

`\begin{gathered} w^2+14w-1632=0 \\ w^2+48w-34w-1632=0 \\ w(w+48)-34(w+48)=0 \\ (w-34)(w+48)=0 \\ w-34=0\text{ and w+48 = 0} \\ w=34\text{ and -48} \end{gathered}`

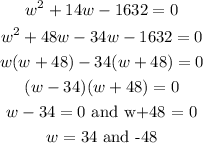
Since the width cannot be negative, hence w = 34 feet.

Recall that A = lw, hence;

`\begin{gathered} l=(A)/(w) \\ l=(1632)/(34) \\ l=48ft \end{gathered}`

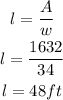
Hence the length and width of the floor are 48feet and 34 feet respectively.