Question

let me know if you need to see the answer choices1) is, or is not 2) -3/2 and 3/4, -3/2 and 2/3, or -4/3 and 3/4 3) are, or are not

Answer 1

Quadrilateral ABCD is not a rectangle because consecutive sides have slopes of 3/4 and -3/2 so they are not perpendicular

1) Considering that to be a rectangle that quadrilateral needs to have perpendicular line segments and two pairs of congruent segments.

2) Let's find the slope of the line segments AB and BC, bearing in mind the coordinates of A(-2,-1) B(2,2) and C(4,-1)

`\begin{gathered} m_(AB)=(2-(-1))/(2-(-2))=(3)/(4) \\ m_(BC)=(-1-2)/(4-2)=(-3)/(2) \\ m_(CD)=(-4-(-1))/(0-4)=(-3)/(-4)=(3)/(4) \\ m_(AD)=(-4-(-1))/(0-(-2))=(-3)/(2) \end{gathered}`

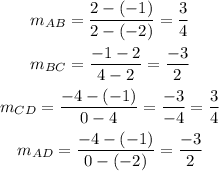
Note, that in order to state that there are perpendicular lines, the slope of AB and BC should be the opposite and reciprocal so AB is 3/4 and BC should be -4/3. The same does not occur to AB and AD.

3) Hence, the answer is:

Quadrilateral ABCD is not a rectangle because consecutive sides have slopes of 3/4 and -3/2 so they are not perpendicular