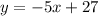For Parallelism condition, the slope of the two(2) lines are equal.
i.e:
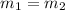
From the given equation of the line:
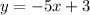
Comparing this with the standard straight line equation: y= mx + c, where m represents the slope, we have:
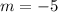
Since the lines are parallel; the new slope is also equal to -5.
Thus,
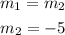
Now that we know the slope and a point (5, -2), we can use the slope formula:
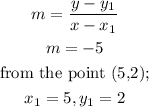
Thus, we have:
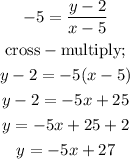
Hence, the equation in slope-intercept form is: