Question

a hydraulic lift requires a minimum effort force force of 14.4N to lift a patient of mass 82kg .How much is the effort piston area if the resistance piston has an area of 1.2m2, assuming the piston are circular

Answer 1

0.022 m²

Step-by-step explanation:

By Pascal's law, we have the following relationship

`(F_1)/(A_1)=(F_2)/(A_2)`

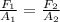
Where F1 is the effort force, A1 is the effort piston area, F2 is the resistance force and A2 is the resistance piston area.

Since the resistance force is the weight of a patient, we get:

F2 = 82kg (9.8 m/s²) = 803.6 N

Now, we can replace F1 = 14.4 N, F2 = 803.6N, and A2 = 1.2 m²

`(14.4N)/(A_1)=(803.6N)/(1.2m^2)`

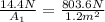
Solving for A1, we get:

`\begin{gathered} 14.4(1.2)=803.6(A_1) \\ 17.28=803.6A_1 \\ (17.28)/(803.6)=A_1 \\ 0.022=A_1 \end{gathered}`

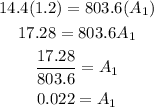
Therefore, the area of the effort piston area should be 0.022 m²