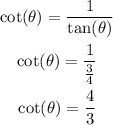First, we need to find the length of the hypotenuse. The Pythagorean theorem states:
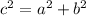
where a and b are the legs and c is the hypotenuse of a right triangle.
Substituting with a = 21 and b = 28, we get:
![\begin{gathered} c^2=21^2+28^2 \\ c^2=441+784 \\ c^2=1225 \\ c=\sqrt[]{1225} \\ c=35 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/o0efgvow5cdeskgsufeyztw8q9p2eai5gk.png)
The length of the hypotenuse is 35.
Sine formula
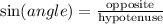
Considering angle θ, the opposite leg is 21. Therefore:
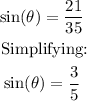
Cosine formula
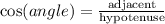
Considering angle θ, the adjacent leg is 28. Therefore:
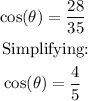
Tangent formula
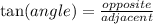
Considering angle θ, the adjacent leg is 28 and the opposite leg is 21. Therefore:
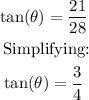
Secant formula
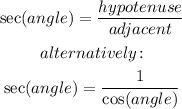
Substituting with the cosine value previously found:
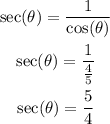
Cosecant formula
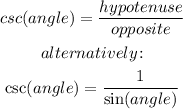
Substituting with the sine value previously found:
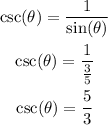
Cotangent formula
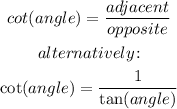
Substituting with the tangent value previously found: