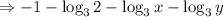The equation is given to be:
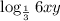
Recall the logarithm rule:
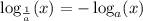
Therefore, the expression becomes:
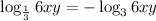
Factorize the number 6:
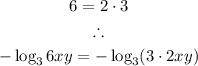
Recall the rule of logarithm:
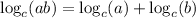
Thus, the expression becomes:
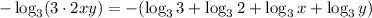
Recall the rule:
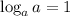
Hence, the expression simplifies to give:
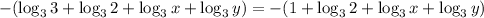
Expanding, we have the answer to be: