Question

The population of the world in 1987 was 5 billion and the annual growth rate was estimated at 1.6% per year. Assuming that the world population follows an exponential growth model, find the projected world population in 2017. Round your answer to 1 decimal place.

Answer 1

The form of an exponential growth model is:

`y=y_0e^(rt)`

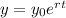
Where:

• y0 is the initial population

,

• r is the rate of annual growth, in decimal

,

• t are years since 1987

In this case:

y0 is 5 billion.

The annual growth rate is 1.6%. To covert to decimal, we divide by 100:

`(1.6)/(100)=0.016`

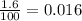
r = 0.016

And t are the years since 1987. We want to find the population in 2017. Then:

`t=2017-1987=30`

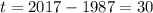
We can construct the model equation:

`y=5,000,000,000e^(0.016\cdot30)`

And solve:

`y=8,080,372,011`

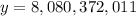
This is the projected world population in 2017