Question

Write the equation of an ellipse in standard form, and identify the end points of the major and minor axes as well as the foci. #23

Answer 1

`\begin{gathered} ((x+5)^2)/(5^2)+((y-2)^2)/(2^2)=1 \\ \text{end points of the major axis }=(0,2),(-10,2) \\ \text{end points of the minor axis }=(-5,4),(-5,0) \\ f=(-5+\sqrt[]{21},2),(-5-\sqrt[]{21},2) \end{gathered}`

Explanation:

We have the following equation of the ellipse in its standard form:

`4x^2+40x+25y^2-100y+100=0`

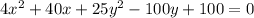
We convert this equation to the general form of an equation of an ellipse with no center at the origin, like this:

`\begin{gathered} 4x^2+40x+25y^2-100y=-100 \\ 4\cdot(x^2+10x)+25\cdot(y^2-4y)=-100 \\ \text{ We divide by 4} \\ (x^2+10x)+(25)/(4)\cdot(y^2-4y)=-25 \\ \text{ We divide by 25} \\ (1)/(25)(x^2+10x)+(1)/(4)\cdot(y^2-4y)=-1 \\ \text{ We complete both squares} \\ (1)/(25)(x^2+10x+25)+(1)/(4)\cdot(y^2-4y+4)=-1+(1)/(25)\cdot25+(1)/(4)\cdot4 \\ (1)/(25)(x+5)^2+(1)/(4)(y-2)^2=-1+1+1 \\ ((x+5)^2)/(25)+((y-2)^2)/(4)=1 \\ ((x-(-5))^2)/(5^2)+((y-2)^2)/(2^2)=1 \end{gathered}`

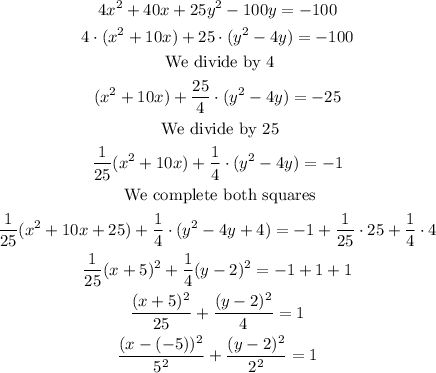
We have that the equation in its general form is the following:

`\begin{gathered} (\mleft(x-h\mright)^2)/(a^2)+(\mleft(y-k\mright)^2)/(b^2)=1 \\ \text{ Therefore, in this case:} \\ h=-5 \\ k=2 \\ a=5 \\ b=2 \\ \text{end points of the major axis }=(-5+5,2),(-5-5,2)\rightarrow(0,2),(-10,2) \\ \text{end points of the minor axis }=(-5,2+2),(-5,2-2)\rightarrow(-5,4),(-5,0) \end{gathered}`

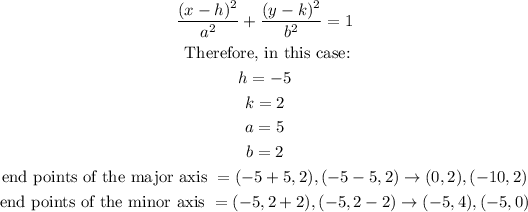
Now, we calculate the focus of the ellipse just like this:

`\begin{gathered} c^2=a^2-b^2 \\ c=\sqrt[]{5^2-2^2} \\ c=\sqrt[]{25-4} \\ c=\sqrt[]{21} \\ \text{ Therefore, the foci is:} \\ f=(-5+\sqrt[]{21},2),(-5-\sqrt[]{21},2) \end{gathered}`