Hello there. To solve this question, we'll have to remember some properties about system of equations.
Given the following system of equations:
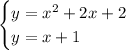
In the R² plane, we have that the solutions to this system are the points of intersection of the parabola y = x² + 2x + 2 and the line y = x + 1.
In fact, there must be two points of intersection and, therefore, two solutions for this system of equation.
Let's plug the first equation into the second equation (called the method of substitution):
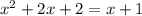
Subtract x + 1 on both sides of the equation

Now, this is a quadratic equation of the form:
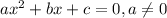
Its solutions are given by the quadratic formula:
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
Plugging the coefficients a = b = c = 1, we get:
![x=\frac{-1\pm\sqrt[]{1^2-4\cdot1\cdot1}}{2\cdot1}](https://img.qammunity.org/2023/formulas/mathematics/college/j53uhm8ps54sl1194tu4cukpu2xw9ww2zc.png)
Square the number and multiply the values. Add everything inside the radical.
![x=\frac{-1\pm\sqrt[]{1-4}_{}}{2}=\frac{-1\pm\sqrt[]{-3}_{}}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/uoejdy9wyltejt29uchzlydbzgdfqmagsa.png)
In this case, we got a negative number inside the square root. This is not defined in the real numbers, therefore we don't have solutions for this system of equations.
Graphically, and this is why I omitted it from the beginning, is that in fact the parabola and the line won't have any intersection points, as you can see in the following image:
If we were to solve this system of equations in the set of the complex numbers, then we would have solutions.
First, remember:
![\sqrt[]{-1}=i](https://img.qammunity.org/2023/formulas/mathematics/high-school/6auedmvsax8nlo4hpms2kngcv15a6lmlel.png)
Such that:
![x=\frac{-1\pm\sqrt[]{-3}}{2}=\frac{-1\pm\sqrt[]{3}\cdot\sqrt[]{-1}}{2}=\frac{-1\pm\sqrt[]{3}i}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/1kt1ic7ged6wvfmipdm0s4w6qp0q443km1.png)
And the values of y can be found by plugging it in the second equation (the easier one)
![y=\frac{-1\pm\sqrt[]{3}i}{2}+1=\frac{-1\pm\sqrt[]{3}i+2_{}}{2}=\frac{1\pm\sqrt[]{3}i}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/88eyc8q1e0dcw5ij123gjeyazurk8t9y42.png)
And the ordered pairs (x, y) would have been:

But as we're talking about real numbers, we say that this is an impossible system of equations, that has no solutions.