Question

The bullseye of a dart board is directly across from the dart being thrown, S. / maway. If the dart is released at 21.3 m/s horizontally. Does the dart hit within 1.00cm of the bullseye? It not, how should the shot be adjusted?

Answer 1

The dart won't hit within 1.00 cm of the bullseye

Step-by-step explanation:

First, we need to calculate the time that the dart takes to hit the dartboard. This can be calculated using the distance of 5.7 m and the horizontal speed of 21.3 m/s, so

`\begin{gathered} v=(d)/(t) \\ \\ t=(d)/(v)=\frac{5.7\text{ m}}{21.3\text{ m/s}}=0.268\text{ s} \end{gathered}`

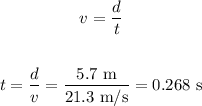
Then, with this time we can calculate the change in height of the dart, using the following equation

`\Delta y=v_0t-(1)/(2)gt^2`

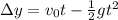
Where vo is the initial vertical velocity, so vo = 0 m/s, g is the gravity, so g = 9.8 m/s², and t is 0.268 s.

So, replacing the values, we get:

`\begin{gathered} \Delta y=0(0.268)-(1)/(2)(9.8)(0.268)^2 \\ \Delta y=0.3509\text{ m} \\ \Delta y=35.09\text{ cm} \end{gathered}`

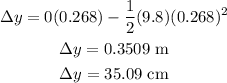
Since Δy is greater than 1 cm, the dart will not hit within 1.00 cm of the bullseye. So, to adjust the shot, you should release the dart from 35.09 cm above.