Question

For the following relation, give the domain and range, and indicate whether it is a function.{(1, 2), (7, 8), (6, 4), (7,5)}Domain: {Range:{Is it a function?Select an answeryesno

Answer 1

We have the following relation, given as follows:

`\lbrace(1,2),(7,8),(6,4),(7,5)\rbrace`

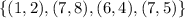
And we need to find the domain and the range of that relation, and determine if the given relation is a function.

1. To find the domain, we already know that the domain of a relation (or a function) is the set of all the inputs. In this case, the inputs are given by the first element of the coordinates pairs: 1, 7, 6, 7. However, since in a set we do not repeat the given values, then the elements of the domain are:

`\text{ Domain:}\lbrace1,6,7\rbrace`

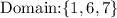
2. To find the range in the given relation, we can proceed in a similar way as before. However, we need to select the second element of the given coordinate pairs: 2, 8, 4, and 5.

We know that the range of a function is the set of outputs of the relation (or of a function). That is, after following the rule of the function, we get the result, and this result will be the range of the relation (or of a function). Therefore, the range can be written as:

`\text{ Range: }\lbrace2,4,5,8\rbrace`

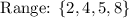
3. To determine if the relation is a function, we need to remember that the key fact that makes a relation a function is that there will be exactly one output for each input.

In this case, we can see that input 7 has two outputs: 8 and 5. Therefore, this relation is NOT a function.

And we can see that, graphically, as follows:

Therefore, in summary, we have:

• Domain: {1, 6, 7}

,

• Range: { 2, 4, 5, 8}

,

• Is it a function?: No