Question

What are the zeros of the function f(x) = (2x+6)(x-4)?A. X = 6 and x = -4B. x = 3 and x = -4C. x = -3 and x = 4D. X=-6 and x = -4

Answer 1

The zeroes of the function are the values of x which make it equal to zero

Since f(x) = (2x + 6)(x - 4)

Then to find the zeroes of f, equate f(x) by 0

`\begin{gathered} f(x)=0 \\ (2x+6)(x-4)=0 \end{gathered}`

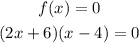
Equate each bracket by 0 to find x

`2x+6=0`

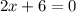
Subtract 6 from each side

`\begin{gathered} 2x+6-6=0-6 \\ 2x=-6 \end{gathered}`

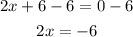
Divide both sides by 2

`\begin{gathered} (2x)/(2)=(-6)/(2) \\ x=-3 \end{gathered}`
`x-4=0`

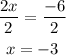
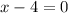
Add 4 to each side

`\begin{gathered} x-4+4=0+4 \\ x=4 \end{gathered}`

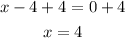
The zeroes of the function are x = -3 and x = 4

The answer is C