Question

Write a system of equations to describe the situation below, solve using any method, and fill in the blanks.The owner of two hotels is ordering towels. He bought 39 hand towels and 43 bath towels for his hotel in Bloomington, spending a total of $426. He also ordered 35 hand towels and 97 bath towels for his hotel in Livingston, spending $908. How much does each towel cost?

Answer 1

Let h and b be the cost for the hand towels and bath towels, respectively. Then, the statement "39 hand towels and 43 bath towels for $426" can be written as

`39h+43b=426`

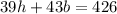
and the statement "35 hand towels and 97 bath towels for $908" can be written as

`35h+97b=908`

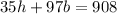
So, we have the following system of equations:

`\begin{gathered} 39h+43b=426 \\ 35h+97b=908 \end{gathered}`

Solving by elimination method.

By multiplying the first equation by -35 and the second one by 39, we have an equivalent system of equations:

`\begin{gathered} -1365h-1505b=-14910 \\ 1365h+3783b=35412 \end{gathered}`

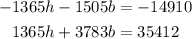
So, we can eliminate variable h by adding both equations, that is,

`2278b=20502`

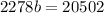
Then, we have

`\begin{gathered} b=(20502)/(2278) \\ b=9 \end{gathered}`

Finally, by substituting this result into the first equation, we get

`39h+43(9)=426`

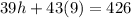
which gives

`\begin{gathered} 39h+387=426 \\ 39h=39 \\ \text{then} \\ h=(39)/(39) \\ h=1 \end{gathered}`

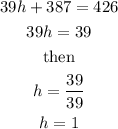
Therefore, the cost for the hand towels is $1 and for the bath towels is $9.