Question

Sal's Sandwich Shop sells wraps and sandwiches as part of its lunch specials. The profit on every sandwich is $2, and the profit on every wrap is $3. Sal made a profit of $1,470 from lunch specials last month. The equation 2x + 3y = 1,470 represents Sal's profits last month, where x is the number of sandwich lunch specials sold and y is the number of wrap lunch specials sold.1) Change the equation to slope-intercept form. Identify the slope and y-intercept of the equation. Be sure to show all your work.2) Describe how you would graph this line using the slope-intercept method. Be sure to write using complete sentences.3) Write the equation in function notation. Explain what the graph of the function represents. Be sure to use complete sentences.4) Graph the function. On the graph, make sure to label the intercepts. 5) Suppose Sal's total profit on lunch specials for the next month is $1,593. The profit amounts are the same: $2 for each sandwich and $3 for each wrap. In a paragraph of at least three complete sentences, explain how the graphs of the functions for the two months are similar and how they are different.

Answer 1

Given

`\begin{gathered} 2x+3y=1470 \\ x\rightarrow\text{ number of sandwiches} \\ y\rightarrow\text{ number of wraps} \end{gathered}`

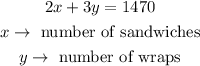
1) Solve for y to find the slope-intercept form, as shown below

`\begin{gathered} \Rightarrow3y=1470-2x \\ \Rightarrow y=(1470)/(3)-(2x)/(3) \\ \Rightarrow y=-(2)/(3)x+490 \end{gathered}`

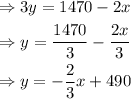
The slope-intercept form of the equation is y=-2x/3+490, where -2/3 is the slope and +490 is the y-intercept.

2) To graph the equation, start at (0,490), the y-intercept; then, move 3 units to the right for every 2 units down because the slope is -2/3.

For example, to the right of (0,490) we can find (0+3,490-2)=(3,488)

3) From part 1), notice that to the right of the equality there are only terms of x; then, we can rewrite it as shown below

`\begin{gathered} y=f(x) \\ \Rightarrow f(x)=-(2x)/(3)+490 \end{gathered}`

The graph of f(x) is the number of wraps as a function of the number of sandwiches (x).

4)

5)

The slope of the two lines will be the same since the ratio cost of a sandwich to the cost of a wrap stays the same; in contrast, the value of the y-intercept will be different because the total profit is now $1593 rather than $1470