We have to find the equation of the hyperbola in standard form.
The information we have is:
• Center: (4, 2)
,
• Vertex: (9, 2)
,
• Focus: (4+√26, 2)
From the center, we can derive the values for h and k, as the center of the hyperbola will be (h,k).
Then, h = 4 and k = 2.
We know have to use the information from the vertex and the focus to find parameters a and b.
We can start sketching the hyperbola and the points as:
As 4+√26 is approximately 9.1, the focus and the vertex are very close, as the vertex has x-coordinate x = 9.
We can now calculate the parameter a using the vertex as:
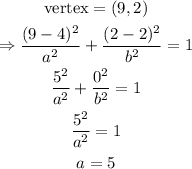
We now have to calculate parameter b.
The only information we haven't used is the focus.
We can relate the focus coordinates to the equation as:

where c is the focal distance.
This focal distance will be, in this case, the distance between the focus and the vertex.
We can express this as:
![\begin{gathered} c=\sqrt[]{(x_v-x_f)^2+(y_v-y_f)^2} \\ c=\sqrt[]{(9-4+\sqrt[]{26})^2+(2-2)^2} \\ c=\sqrt[]{(5+\sqrt[]{26})^2} \\ c=5+\sqrt[]{26} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/3iffwkda72ea9zjervdszlmceezq66svay.png)
We can now calculate b as:
![\begin{gathered} a^2+b^2=c^2 \\ b^2=c^2-a^2 \\ b^2=(5+\sqrt[]{26})^2-5^2 \\ b^2=5^2+2\cdot5\cdot\sqrt[]{26}+(\sqrt[]{26})^2-5^2 \\ b^2=10\sqrt[]{26}+26 \\ b^2\approx77 \\ b\approx\sqrt[]{77} \\ b\approx8.77 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/txkq8doo2eyi0m1teet48o8096nrj33eql.png)
Then, we can complete the equation as:
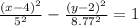
Answer:
h = 4, k = 2, a = 5 and b = 8.77.