Question

The discriminant of ax^2+ bx + c = 0 is defined as? A. 2a B. Square root b^r -4ac

Answer 1

For the general quadratic equation:

`ax^2+bx+c=0`

the solutions are given by the quadractic formula

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

The discriminant tells you how many possible solutions a particular quadratic equation has and is given by the term into the square root:

`b^2-4ac`

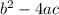
If the discriminant is negative, the quadratic equation has no real solutions because the square root of negative numbers is not defined (yet)

The real solutions correspond to the x-intercepts of a given graph. Then, the answer is: x-intercepts. That is because the equation

`ax^2+bx+c=0`

is the same as

`y=0`

that is, the solutions are the x-values where y is equal to zero, which are the x-intercepts.

In other words, they are the locations where the function crosses or touches the x-axis