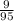Question

A bag contains hair ribbons for a spirit rally. The bag contains 18 black ribbons and 2 green ribbons. Lila selects a ribbon at random, then Jessica selects a ribbon at random from the remaining ribbons. What is the probability that Lila selects a black ribbon and Jessica selects a green ribbon?

Answer 1

Step-by-step explanation:

Given;

We are told that a bag contains the following;

`\begin{gathered} Black\text{ }ribbons=18 \\ \\ Green\text{ }ribbons=2 \\ \\ Total=20 \end{gathered}`

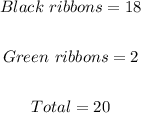
Lila selects a ribbon at random and then Jessica selects a ribbon at random from the remaining ones.

Required;

Calculate the probability that Lila selects a black ribbon and Jessica selects a green ribbon.

Step-by-step solution;

The probability of an event is calculated by the formula given below;

`P[Event]=\frac{number\text{ }of\text{ }required\text{ }outcomes}{number\text{ }of\text{ }all\text{ }possible\text{ }outcomes}`

For Lila to select a black ribbon, we have;

`\begin{gathered} P[black]=(18)/(20) \\ \\ P[black]=(9)/(10) \end{gathered}`

Now we have 19 ribbons left, note that Jessica had to select from the remaining ribbons.

For Jessica to select a green ribbon, we have;

`P[green]=(2)/(19)`

Next to calculate the probability that Lila selects a black ribbon and Jessica selects a green ribbon we have a product of probabilities;

`\begin{gathered} P[black]\text{ }and\text{ }P[green]=(9)/(10)*(2)/(19) \\ \\ P[black]\text{ }and\text{ }P[green]=(9)/(95) \end{gathered}`

Therefore,

ANSWER:

The probability that Lila selects a black ribbon and Jessica selects a green ribbon is,

`(9)/(95)`