Question

Use a system of equations to solve the following problem.The local theater has three types of seats for Broadway plays: main floor, balcony, and mezzanine.Main floor tickets are $52, balcony tickets are $37, and mezzanine tickets are $31. One particularnight, sales totaled $50,512. There were 86 more main floor tickets sold than balcony and mezzaninetickets combined. The number of balcony tickets sold is 139 more than 2 times the number ofmezzanine tickets sold. How many of each type of ticket were sold?

Answer 1

Main floor ticket is $52

Balcony ticket is $37

Mezzanine ticket is $31

Let x represent main floor tickets

Let y represent balcony tickets

Let z represent main mezzanine tickets

On a particular day, total sales totaled $50512, i.e

`\begin{gathered} 52* x+37* y+31* z=50512 \\ 52x+37y+31z=50512\ldots(1) \end{gathered}`

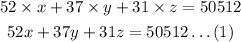
There were 86 more main floor tickets sold than balcony and mezzanine tickets combined, i.e

`\begin{gathered} y+z+86=x \\ x-y-z=86\ldots(2) \end{gathered}`

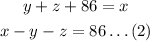
The number of balcony tickets sold is 139 more than 2 times the number of mezzanine tickets sold, i.e

`\begin{gathered} 2z+139=y \\ y-2z=139\ldots(3) \end{gathered}`

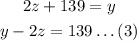
The equatons are

`\begin{gathered} 52x+37y+31z=50512\ldots(1) \\ x-y-z=86\ldots(2) \\ y-2z=139\ldots(3) \end{gathered}`

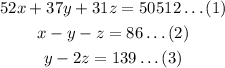
Solving to find the values of x, y and z

From equation (3), make y the subject

`\begin{gathered} y-2z=139 \\ y=139+2z\ldots(4) \end{gathered}`

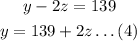
Substitute for y into equation (2)

`\begin{gathered} x-y-z=86 \\ x-(139+2z)-z=86 \\ x-139-2z-z=86 \\ x-139-3z=86 \\ x-3z=225 \end{gathered}`

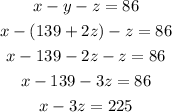
Make x the subject

`\begin{gathered} x-3z=225 \\ x=225+3z\ldots(5) \end{gathered}`

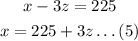
Substitute for x and y into equation (1)

`\begin{gathered} 52x+37y+31z=50512 \\ 52(225+3z)+37(139+2z)+31z=50512_{} \\ 11700+156z+5143+74z+31z=50512 \\ \text{Collect like terms} \\ 156z+74z+31z=50512-11700-5143 \\ 261z=33669 \\ \text{Divide both sides by 261} \\ (261z)/(261)=(33669)/(261) \\ z=129 \end{gathered}`

Substitute for z into equation (5) to find x

`\begin{gathered} x=225+3z \\ x=225+3(129) \\ x=225+387 \\ x=612 \end{gathered}`

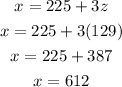
Substitute for z into equation (4) to find y

`\begin{gathered} y=139+2z \\ y=139_{}+2(129) \\ y=139+258 \\ y=397 \end{gathered}`

Hence,

The number of main floor tickets (x) sold is 612

The number of balcony tickets (y) sold is 397

The number of mezzanine tickets (z) sold is 129