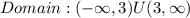Question

I solved this and think the answer is all real numbers except 3. Can you confirm if I solved this correctly? Thanks!

Answer 1

All real numbers except 3

Explanations:

The domain of a function are the independent values of the function for which it exists.

Given the function expressed as:

`f(x)=(13)/(3-x)`

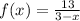
A rational function does not exist if the denominator is zero. For the given function, it tends to infinity when 3 - x = 0

3 - x = 0

x = 3

This shows that the function exists on all real number except 3. The domain of the function in interval form is expressed as:

`Domain:(-\infty,3)U(3,\infty)`