Question

The area of a rectangle is represented by 36 x^{6} y^{4}. One side is represented by 6 x^{3} y^{2}. What is the length of the other side? What does this indicate about the type of rectangle represented?

Answer 1

• 6x³y²

,

• Square

Step-by-step explanation:

Area of a rectangle = Length x Width

If the area and one side of the rectangle is given:

`\begin{gathered} \text{Area}=36x^6y^4 \\ \text{Length}=6x^3y^2 \end{gathered}`

We then have that:

`36x^6y^4=6x^3y^2* Width`

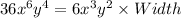
We solve the above for the length of the other side.

`\begin{gathered} \text{Width}=(36x^6y^4)/(6x^3y^2) \\ =6x^3y^2 \end{gathered}`

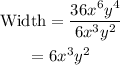
We notice that the length of both sides is the same. Therefore, the type of rectangle represented is actually a square.