Question

Using the Pythagorean theorem decided if the values 10 11 2 could be a right triangle

Answer 1

We have to check if a triangle with sides of length 10, 11 and 2 could be a right triangle.

If it is a right triangle, it should verify the Pythagorean theorem:

`c^2=a^2+b^2`

where c is the hypotenuse, that we can identify as the longest side.

In this case the hypotenuse would be 11, as it is the longest side.

Then, 2 and 10 would be the legs.

We can then check the Pythagorean theorem:

`\begin{gathered} c^2=a^2+b^2 \\ 11^2=10^2+2^2 \\ 121=100+4 \\ 121\\e104\to Not\text{ }verified \end{gathered}`

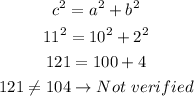
As the sides do not check the Pythagorean theorem, the sides do not correspond to a right triangle.

Answer: The sides do not correspond to a right triangle.