Question

Write an equation of the line passing through the point (4, 3) that is perpendicular to the line Y + 3 = -9/11 (x + 4)

Answer 1

We have to find the equation of a line that pass through the point (4,3) and is perpendicular to the line:

`y+3=-(9)/(11)(x+4)`

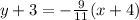
This line, that is perpendicular, has a slope m=-9/11, as it is written in slope-point form.

The line we are looking for will have a slope that is the negative reciprocal of m=-9/11, so it will be:

`m_2=-(1)/(m_1)=-(1)/(-(9)/(11))=(11)/(9)`

Our line has a slope of m=11/9.

We can use the known point (4,3) to write the equation as:

`y-3=(11)/(9)(x-4)`

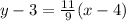
If we want the equation in slope intercept form, we rearrange:

`\begin{gathered} y=(11)/(9)(x+4)+3 \\ y=(11)/(9)x+(44)/(9)+3 \\ y=(11)/(9)x+(44+27)/(9) \\ y=(11)/(9)x+(71)/(9) \end{gathered}`

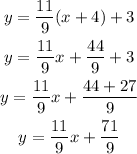
Answer: y-3=11/9*(x-4)