Question

the graph of f passes through (-6,4) and is perpendicular to the line that has an x-intercept of 3 and a y-intercept of-6

Answer 1

To solve this problem, first, we have to find the slope of the line that has an x-intercept of 3 and a y-intercept of 6. The intercepts can be written as (3,0) and (0,6). Let's use the slope formula

`m=(y_2-y_1)/(x_2-x_1)`

Where,

`\begin{gathered} x_1=3 \\ x_2=0 \\ y_1=0 \\ y_2=6 \end{gathered}`

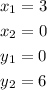
Let's use these values to find the slope.

`m=(6-0)/(0-3)=(6)/(-3)=-2`

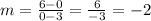
The slope of the line that has the given intercepts is m = -2.

Now, we have to find the perpendicular slope of m = -2 using the following rule

`m\cdot m_{\text{perp}}=-1`

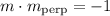
Let's replace the slope we found and find the other one.

`m_{\text{perp}}=-(1)/(m)=-(1)/(-2)=(1)/(2)`

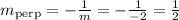
The slope of the perpendicular line is 1/2.

Once we have the slope of the new perpendicular line, we use the point-slope formula

`y-y_1=m_{\text{perp}}\cdot(x-x_1)`

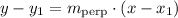
Where,

`\begin{gathered} x_1=-6 \\ y_1=4 \\ m_{\text{perp}}=(1)/(2) \end{gathered}`

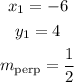
Let's use these values above to find the equation of the new perpendicular line.

`\begin{gathered} y-4=(1)/(2)(x-(-6)) \\ y-4=(1)/(2)(x+6) \\ y-4=(1)/(2)x+(6)/(2) \\ y=(1)/(2)x+3+4 \\ y=(1)/(2)x+7 \end{gathered}`

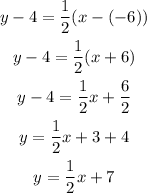
Therefore, the equation of the new perpendicular line that passes through (-6,4) is

`y=(1)/(2)x+7`

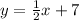
The image below shows the graph of this function