Question

which statements about the line that passes through (-2,0) and (2,-4) are true? select all that apply

Answer 1

For this case we have the following points given:

`(x_1=-2,y_1=0),(x_2=2,y_2=-4)`

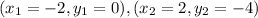
And the slope is given by:

`m=(y_2-y_1)/(x_2-x_1)`

And replacing we got:

`m=(-4-0)/(2-(-2))=(-4)/(4)=-1`

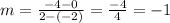
The equation for the line is be given by:

`0=-1(-2)+b`
`b=-2`

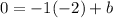
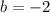
And the equation would be given by:

`y=-x-2`

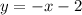
And the intersection points would be:

x=0 y=-2. (y intercept)

y=0, x=-2. (x intercept)

The best answer would be:

B , C and D