Given the line equation
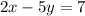
Let's consider a generic line with coefficients
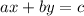
The perpendicular line will be
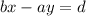
Fact, we just need to change the coefficients and the ONLY one signal. Then, again, given
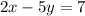
We need to change the x and y coefficient:
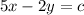
Now we change the signal of the coefficient with "y"
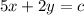
The value of c here doesn't matter, just the coefficients, then, the final answer is
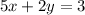
That's the line equation perpendicular to the line 2x – 5y = 7