Step-by-step explanation:
To determine the equation of line perpendicular to the line on the graph, first we need to find the slope of the line on the graph.
We pick any two points on the line: (-4, 4) and (4, -2)
Applying slope formula:
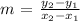
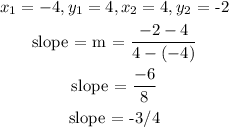
For one line to be perpendicular to another line, the slope of one line will be the negative reciprocal of the second line.
We know the slope of one of the line = -3/4
recirocal of the slope = 4/-3 = -4/3
negative reciprocal = -(-4/3) = 4/3
This means the slope of the second line = 4/3
We have been told the second line has x intercept of 6.
x-intercept is the value of x when y = 0
Equation of line:
y = mx + b
m
We would use the slope of this line and the x intercept to get b (the y-intercept)